CHƯƠNG TRÌNH IGCSE MATHS 0580 CỦA CAMBRIDGE THAY ĐỔI

https://www.facebook.com/share/p/DSMatrgcBRZtEbwE/

Những ngày vừa qua, các con đang vào mùa thi IGCSE Cambridge. Riêng môn Maths đã thi xong và cũng kết thúc kỳ thi đợt mùa Xuân cuối cùng theo syllabus 2024.

Năm sau, Cambirdge sẽ ra đề thi với syllabus mới, áp dụng từ năm 2025 đến 2027.

Trong status này, tôi trình bày các điểm thay đổi cơ bản của syllabus mới so với syllabus 2023-2024 và phân tích ảnh hưởng của nó đến các con em chúng ta. Ở đây, tôi chỉ tập trung vào Extended vì hầu hết các con đều thi ở nội dung này

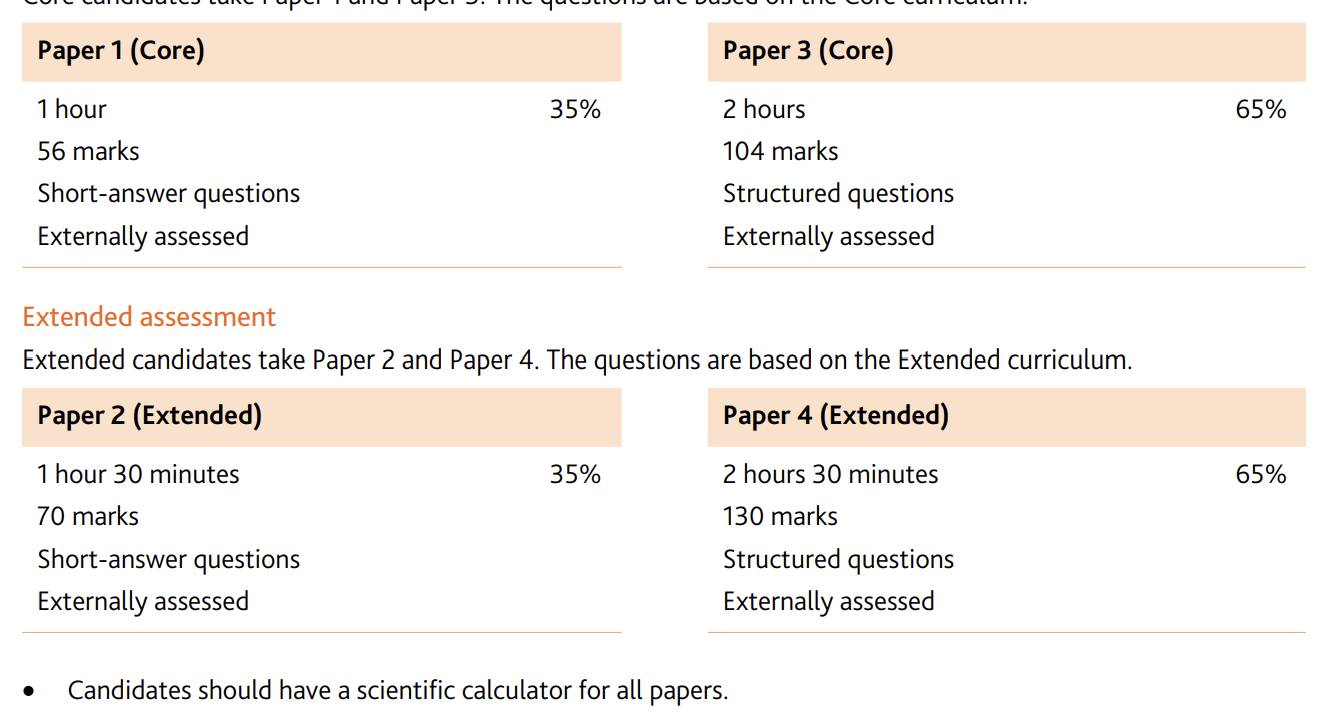
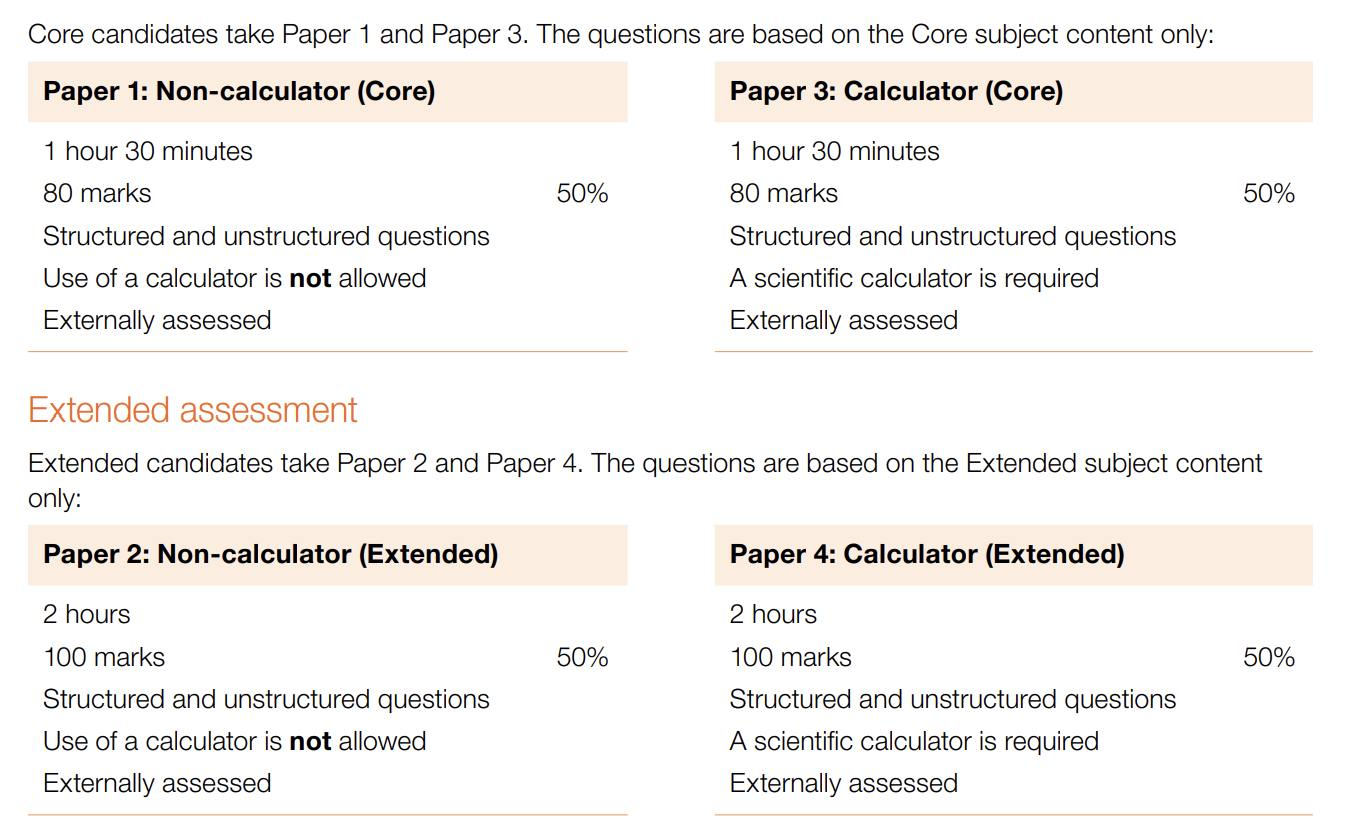
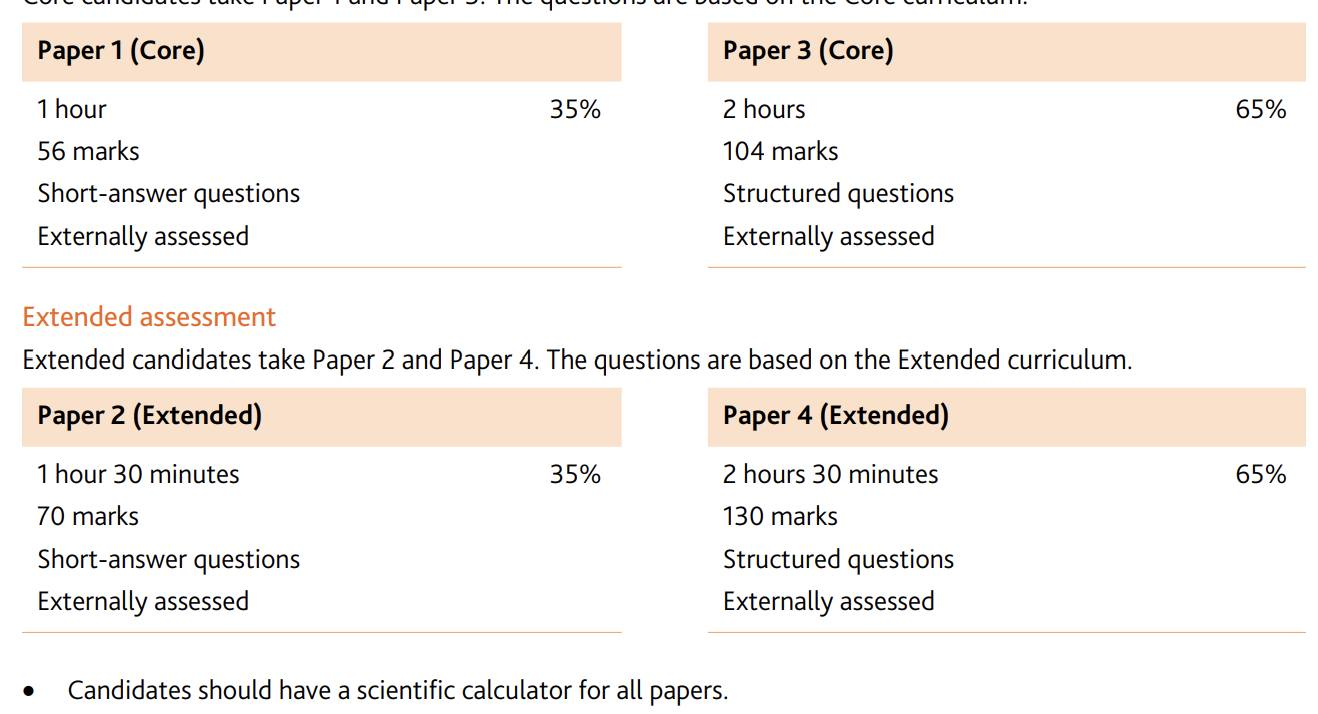
Trước hết, về hình thức, các con vẫn thi 2 Papers (2 và 4) nhưng:

Papers 2 không cho dùng máy tính cầm tay, số điểm tối đa tăng lên đến 100 và thời gian kéo dài lên đến 2 giờ. Trong khi đó Paper 2 cũ cho dùng máy tính, số điểm tối đa chỉ là 70 và thời gian làm bài 90 phút.

Đây là sự thay đổi đáng kể, đặc biệt với các con không quen tính toán tay, phụ thuộc nhiều vào máy tính. Mà cái vụ “nô lệ máy tính” này thì tôi thấy rất nhiều. Các con lệ thuộc đến mức khi gặp một số phép tính rất đơn giản cũng phải nhờ trợ giúp của Casio. Nếu không cải thiện khả năng tính tay thì các con sẽ rất khó khăn khi làm Paper 2.

Paper 2 cũ chỉ có 70 điểm so với Paper 4 có 130 điểm. Vì thế nội dung Paper 2 cũ thường là các bài toán đơn giản, có tính chất kiểm tra kiến thức cơ bản. Do vậy, các con thường thích Paper 2 và cố gắng lấy điểm nhiều nhất có thể ở Paper này nhằm bù cho sự mất điểm ở Paper 4. Nay thì Paper 2 và Paper 4 có số điểm ngang nhau, độ khó các bài toán ở hai Paper sẽ không chênh lệch nhiều. Cộng thêm ràng buộc không được dùng máy tính, coi bộ Paper 2 trở nên khó nuốt hơn hẵn

Paper 4 vẫn cho dùng máy tính, số điểm tối đa chỉ còn 100 và thời gian thi chỉ còn 2 giờ.

Hình 1 và 2 cho thấy sự thay đổi về hình thức thi.

Về nội dung cũng có sự thay đổi đáng kể.

Sự thay đổi đầu tiên là syllabus mới thêm phần surds. Đây là phần yêu cầu các con nắm kỹ thuật xử lý (tính toán, đơn giản, khai triển...và biết dùng lượng liên hợp để hữu tỷ hóa mẫu số) các biểu thức vô tỷ dưới dạng căn thức. Phần này đòi hỏi các con phải có thời gian làm quen và luyện tập khá nhiều. Các kỹ thuật này nhìn chung không thể dùng Casio hỗ trợ dẫu là các con đang làm Paper 4.

Sự thay đổi thứ hai là yêu cầu các con biết dùng các giá trị chính xác của các hàm lượng giác (chẳng hạn sin 60 = 0 chứ không phải bấm máy tính ra giá trị thập phân). Cái này khác với thói quen dùng Casio của các con và đi kèm với nó là kỹ thuật xử lý surds nói ở trên.

Đồ thị của hàm thì thêm hai đồ thị. Gọi là chỉ thêm hai hàm nhưng bài thi lại cho phép ra đề ghép các hàm khác với hai hàm này nên sinh ra thêm một số tổ hợp hàm buộc các con phải làm quen.

Chủ đề hàm số thêm phần hiểu và chỉ ra domain và range của f(x). Đây là phần không dễ. Trước kia, phần này nằm ở chương trình AS level. Dẫu Cambridge giới hạn tính domain và range cho hàm đơn, không yêu cầu hàm hợp nhưng thực ra bài toán này vẫn đặc biệt khó khi cho một domain giới hạn và tìm range trong domain giới hạn đó.

Syllabus mới bỏ phần linear programming. Phần này thực sự khó hiểu và khó làm. Mừng cho các con không nắm nổi phần này và chia buồn các con nào đã làm chủ phần này (năm lớp 9) mà nay không có đất để thi thố.

Cũng bỏ luôn phần congruence critea (điều kiện hai tam giác bằng nhau). Hơi tiếc cho các con đã học.

Nội dung xác suất và thống kê thì bỏ phần data collection và box-and-whisker plots. Quá tiếc vì hai phần này dễ kiếm điểm.

Các điểm kể trên là những thay đổi chủ yếu của syllabus Maths 0580. Theo chủ quan của mình, tôi cho rằng với những sự thay đổi như vậy, đề thi IGCSE 0580 kể từ tháng 5/2025 sẽ khó hơn đối với hầu hết các con em chúng ta.

Theo ước lượng của tôi thì một học sinh không luyện tập đủ đáp ứng theo syllabus mới thì khi thi có khả năng mức điểm giảm cấp (A* sẽ bị xuống A, A bị xuống B...)

Chương trình VinSchool hệ B đã cập nhật theo syllabus mới này.

Chương trình VinSchool hệ A vẫn dạy theo syllabus cũ. Điều này cũng dễ hiểu vì nhà trường không hề đặt mục tiêu học sinh hệ chuẩn thi Cambridge. Hơn nữa, không thể dịch nhanh và in ấn tài liệu học theo syllabus mới trong thời gian ngắn. Vì vậy, nếu các phụ huynh nào muốn con mình đang học hệ A thi IGCSE thì phải bổ túc cho cháu.

Chương trình trường Royal vẫn theo syllabus cũ. Điều này đáng ngạc nhiên.

Còn các trường khác thì tôi không có thông tin...

Status này không bàn sự hợp lý của việc thay đổi syllabus, cũng như tại sao trường này, trường nọ không dạy theo syllabus mới nhất. Nó chỉ cung cấp thông tin để các phụ huynh hiểu hơn và nếu cần, phụ huynh có những biện pháp bổ túc cho con em mình nếu muốn cháu thi nhằm lấy một chứng chỉ quốc tế về Maths.

Có vẻ hơi lạc lõng khi đến đây tôi lại muốn nhắc lại một câu chuyện đức Phật kể cho các đệ tử nghe trong bài Tiểu kinh Malunkya (bài kinh số 63 – Trung bộ kinh). Đức Thế Tôn kể rằng có một người bị mũi tên tẩm độc bắn. Mọi người muốn mời một y sĩ đến săn sóc nhưng người ấy nói rằng: “Tôi sẽ không rút mũi tên ra khi nào tôi chưa biết được người bắn tôi là thuộc giòng tộc nào, là người da đen hay da vàng, thuộc làng nào, thị trấn nào, bắn bằng loại cung nào, dây cung làm bằng chất liệu gì, mũi tên thuộc loại gỗ nào, lông trên mũi tên lấy từ lông con vật nào...” Và trong khi chờ đợi những câu trả lời cho thỏa lòng mình, người ấy đã chết mà vẫn chưa biết được gì.

Hãy chủ động tự mình tìm cách giúp con hơn là cố gắng thay đổi cả một hệ thống để làm việc đó.

Vesak, 2024

VÌ SAO KỲ THI TOÁN GCSE CAMBRIDGE YÊU CẦU THÍ SINH KHÔNG ĐƯỢC DÙNG MÁY TÍNH CẦM TAY? (Phần1)

(Status này hơi dài, phải chia làm nhiều phần)

Khi biết hội đồng thi Cambridge quyết định đổi hình thức thi Paper 2 GCSE thành bài thi không được dùng máy tính cầm tay, một số học sinh và cả phụ huynh tỏ ra hoang mang. Các con và phụ huynh phản biện rằng vào thời đại số như hiện nay, tại sao lại bắt thí sinh phải tính toán tay, chẳng phải hội đồng thi đã đẩy lùi công nghệ đến vài chục năm. Việc gì phải mất thời gian tính tay một bài toán khi chỉ cần một vài phím bấm là đủ?

Cũng có phụ huynh đồng tình với quy định trên nhưng chia sẻ: “Em hiểu nhưng thật khó giải thích cho con em hiểu được quy định này.”

Một phụ huynh gợi ý cách giải thích với trẻ như sau: “Nếu một ngày nào đó, con lạc vào một hoang đảo hay một vùng đất xa xôi, không máy tính, không điện thoại như Robison Crusoe phải tự mình xoay xở, tồn tại. Lúc đó, mọi tính toán về xác định phương hướng, thời gian, đóng thuyền vượt biến... đều trông cậy vào trí tuệ và đôi tay của mình.” Lý do hợp lý nhưng tình huống đặt ra quá hiếm hoi nên cũng khó thuyết phục con em. Cách giải thích này làm tôi nhớ tới câu hỏi một số bạn: “Nếu mọi người trên thế giới này đều cạo râu tóc, sống không gia đình, phát nguyện đi tu cả thì nòi giống con người sẽ bị hủy diệt. Vậy có nên khuyến khích hạnh xuất gia không?”. Câu trả lời đơn giản: “It’s impossible”. Mơ ước toàn bộ chúng sinh đều đi tu còn khó hơn vạn lần nhiệm vụ trong Mission: Impossible – một series phim rất lôi cuốn nhưng tình tiết cũng … xạo như phim do ngôi sao Tom Cruise thủ vai chính.

Status này trình bày quan điểm của tôi về nguyên nhân chúng ta bắt buộc phải dạy cho con em thành thạo giải toán bằng tay. Những lý do này có thể dễ hiểu đối với người lớn chúng ta nhưng chưa chắc trở thành căn cứ cho lập luận thuyết phục và động viên các cháu rời xa máy tính. Vì vậy ở phần cuối status, ta thử tìm một câu trả lời riêng cho các cháu.

Cần lưu ý rằng không chỉ Cambridge mà nhiều chương trình thi khác cũng đòi hỏi thí sinh tính toán tay. Các nhà toán học và các thầy giáo không ngờ nghệch đến mức đặt ra quy định này chỉ để gây khó cho học sinh.

Lý do thứ nhất liên quan đến việc giúp học sinh hiểu và nhớ các khái niệm quan trọng trong toán học. Tôi xin được kể một câu chuyện có thật. Biết tôi thích cà phê, một người bạn rủ tôi ghé thăm người quen vừa sắm dàn pha cà phê hiện đại. Bước vào ngôi nhà ở trung tâm thành phố, người chủ nhà béo tốt, thân thiện, xởi lởi tiếp đón và đưa chúng tôi vào phòng khách sang trọng. Ở góc phòng là dàn máy nhãn hiệu Ý sáng loáng, hoành tráng. Anh trịnh trọng lấy ra bịch nguyên liệu mà theo anh phải dùng với dàn máy này. Anh bỏ nguyên liệu vào và bấm máy. Sau 5 phút, chúng tôi đã có những ly cà phê nóng hổi. Cà phê rất ngon với vị đặc biệt. Anh và chúng tôi ngồi ở ban công, vừa thưởng thức cà phên vừa nhìn dòng người hối hả qua lại trên con đường phủ đầy bóng mát bởi tàn cây cổ thụ bên đường. Những tưởng chúng tôi sẽ bàn về nguyên liệu cà phê, cách pha chế cũng như mùi vị và hương thơm cà phê đang quyện lấy và làm thăng hoa tâm hồn người uống. Tôi ngỡ ngàng nhận ra anh không biết gì, thậm chí không phân biệt được thế nào là Robusta và Arabica. Mọi việc với anh chỉ đơn giản là mua đúng gói nguyên liệu, bỏ vào máy và bấm nút. Cuộc trò chuyện trở nên rời rạc, uể oải và anh nhanh chóng chuyển qua đề tài khoe dàn âm thanh trị giá vài tỷ vừa sắm được. Ngồi đối diện, miễn cưỡng nghe anh huyên thuyên về dàn ampli, sợi dây dẫn âm thanh chục nghìn USD, tôi buồn rầu nhìn mấy cái nọng mỡ trồi lên sụt xuống ở cổ họng cùng những giọt mồ hôi chảy dài trên cặp má phinh phíng đỏ hồng của anh...

Mọi ngành nghề đều có những khái niệm của nó. Dân trong ngành định nghĩa một khái niệm và đặt tên cho nó nhằm tạo ra một sự phân biệt rõ ràng với các sự vật khác. Các khái niệm sẽ được liên kết với nhau bằng chuỗi lý luận, tạo ra một hệ thống kiến thức đặc thù của ngành. Hiểu và nắm chắc các khái niệm là điều kiện cơ bản để đi vào một ngành học. Người ta gọi tên phương trình bậc hai (quadratic equation) là để phân biệt nó với vô vàn khái niệm khác như phương trình bậc nhất (linear equation), phương trình bậc ba (cubic equation), bất phương trình (inequality)... Bản thân phương trình bậc hai cũng hàm chứa bên trong nó nhiều khái niệm con như phương trình bậc hai không đầy đủ có hệ số b = 0, phương trình bậc hai không đầy đủ có hệ số c = 0... Nếu con em chúng ta chỉ biết tìm nghiệm của một phương trình bậc hai bằng cách bấm máy tính thì khả năng hiểu khái niệm phương trình bậc hai cùng với các khái niệm con của nó dường như không có! Hệt như anh chàng nọ chỉ biết bấm nút ra ly cà phê mà hoàn toàn không biết gì đến các khái niệm về các chủng loại cà phê. Cũng vậy, thay vì cho phép học sinh dùng phần mềm Desmos vẽ graph các hàm (Desmos vẽ vừa nhanh vừa đẹp và chính xác) thì Cambridge yêu cầu các con lập bảng giá trị (table of values), xác đinh từng điểm (point) trên mặt phẳng Oxy rồi nối chúng lại. Có làm bằng tay như vậy thì các con mới nhớ và hiểu sâu sắc rằng đồ thị là tập hợp của các điểm, nhớ khái niệm tọa độ x và tọa độ y (x coordinates and y coordinates) của một điểm. Có nối các điểm bằng một đường cong trơn (smooth) với bàn tay có phần run rẩy, thận trọng thì các con mới hiểu và thấm được tính liên tục (continuity) của một đồ thị. Rồi nếu đồ thị có các tiệm cận (asymptote) thì còn gì hay hơn để các con nhớ khái niệm tiệm cận khi các con bậm môi cố vẽ đồ thị ngày càng tiến sát gần đường tiệm cận nhưng không được chạm vào chúng!

(còn tiếp...)

VÌ SAO KỲ THI TOÁN GCSE CAMBRIDGE YÊU CẦU THÍ SINH KHÔNG ĐƯỢC DÙNG MÁY TÍNH CẦM TAY? (Phần 2)

https://www.facebook.com/share/p/VF8AfxyoQPsCpsaK/

Nhắc lại ở phần 1, một lý do quan trọng yêu cầu học sinh phải làm toán bằng tay là nhằm tạo cơ hội cho các con trải nghiệm và nắm vững những khái niệm cơ bản. Xin cho phép người viết lan man đến việc tu tập Phật giáo. Phần lớn mọi người đến chùa để tụng kinh. Tụng kinh hằng ngày mà không hề biết ý nghĩa của bài kinh! Đã từ lâu, mọi người đồng nhất những bài kinh dài dằng dặc như một phím bấm vạn năng đưa họ đến sự giải thoát, giác ngộ. Tiếc thay, những bài kinh thường đọc trong các chùa (kinh Pháp Hoa, kinh Lăng Nghiêm...) lại là các kinh thuộc truyền thống Đại thừa. Tôi không dám chê bai gì đến các kinh này. Nhưng kinh điển Đại thừa thường khó hiểu. Khó hiểu vì giáo nghĩa Đại thừa căn bản dựa trên triết lý tính Không của hệ Bát nhã mà tính Không lại là một khái niệm rất thâm sâu, vi diệu khiến người căn bản còn kém vô phương hiểu thấu. Mặt khác, kinh Đại thừa vốn sử dụng hình ảnh ẩn dụ, trừu tượng rất cao càng làm việc hiểu giáo nghĩa thêm vô vàn khó khăn. Muốn hiểu tính Không, người học cần nắm những khái niệm căn bản của triết học Phật giáo như ngũ uẩn, sáu căn, sáu trần, tứ diệu đế, bát chánh đạo... Đọc kinh mà không hiểu Pháp thì làm sao hành Pháp? Nguy cơ người đọc kinh trở thành tù nhân của chính mong mỏi giải thoát của mình, ngày càng u mê, lầm lạc là điều hoàn toàn có thể xảy ra.

Lý do thứ hai liên quan đến phương pháp giải quyết vấn đề. Trở lại ví dụ phương trình bậc hai. Chúng ta đều biết để tính nghiệm của phương trình bậc hai, ta có nhiều cách trong đó có ba cách cơ bản: phương pháp phân tích ra nhân tử (factorization), phương pháp đưa về dạng bình phương hoàn chỉnh (completing the squared form) và phương pháp dùng công thức bậc hai (quadratic formula). Mỗi phương pháp đều có ưu và nhược điểm của riêng nó. Ngoài ra, một phương trình bậc hai không đầy đủ (trường hợp đặc biệt b = 0, c= 0...) cũng có cách giải nhanh của chính mình. Giải một phương trình bậc hai bằng tay đòi hỏi các con phải nhận dạng nhanh phương trình cần giải và chọn cho mình cách tối ưu trong các cách đã biết. Điều này hoàn toàn khác hẳn với việc bấm nút giải bằng máy tính, theo đó các con chỉ nhận được nghiệm của phương trình cần giải mà hoàn toàn không biết máy tính đã làm gì để có được các nghiệm này. Bấm nút để có được ly cà phê mà không hiểu từng công đoạn dàn máy đã làm gì và tại sao máy phải làm thế. Một ngày nào đó khách muốn thay đổi hương vị cà phê, muốn thêm một chút chua, một chút đắng, một chút thơm... tôi tin chắc anh chàng kia không biết phải làm gì. Một trong những nhiệm vụ quan trọng của môn toán là thông qua việc học các giải toán, con em chúng ta học cách giải quyết vấn đề. Các con cần hiểu rằng đứng trước một trở ngại trong công việc, các con phải nhận dạng được trở ngại đó, đặt câu hỏi đúng và lựa chọn phương pháp tốt nhất trong hoàn cảnh hiện tại để vượt qua chúng.

(còn tiếp...)

VÌ SAO KỲ THI TOÁN GCSE CAMBRIDGE YÊU CẦU THÍ SINH KHÔNG ĐƯỢC DÙNG MÁY TÍNH CẦM TAY? (Phần 3)

https://www.facebook.com/share/p/YHTyetmTW6APKoTv/

Trong đời sống hằng ngày, dẫu làm ngành nghề gì, chúng ta thường xuyên tiếp xúc với các con số. Cũng như một cầu thủ bóng đá rất cần cái “cảm giác bóng” thì chúng ta sẽ làm việc tốt hơn với con số nếu có “cảm giác số”tốt. Việc lệ thuộc quá sớm vào máy tính sẽ ngăn cản các con “thân thiện” với con số, triệt tiêu cái “cảm giác số” và đôi khi làm các con mất cơ hội khám phá ra những điều thú vị ẩn chứa trong chúng. Thử quan sát một đoạn đối thoại tưởng tượng giữa thầy và trò trong tiết học “Phân số và số thập phân” (Fractions and decimals) thuộc chương trình Cambridge Lower Secondary Mathematics grade 8.

Thầy:

- Con đã biết cách đổi một phân số thành số thập phân.

Trò (hăng hái):

- Dạ. Con lấy tử số chia cho mẫu số.

Thầy:

- Con hãy chuyển phân số ½ ra số thập phân.

...

Thầy:

- Giỏi. Con ra kết quả là 0.5. Bây giờ con đổi tiếp phân số ¾ .

Trò (thực hiện bằng tay phép chia 3 cho 4 , lâu hơn một chút so với trường hợp đầu)

Thầy:

- Giỏi. Bây giờ con làm tiếp cho phân số 1/3

Sau một lúc nỗ lực, trò tính ra trên giấy: 0.3333...

Thầy:

- Phép chia này dường như không kết thúc. Ta nói 1/3 = 0.333.... với chữ số 3 xuất hiện hoài không dứt. Đúng không con?

Trò:

- Dạ đúng

Thầy:

- Bây giờ con lại đổi phân số 5/11 ra số thập phân.

Sau một lúc thực hiện phép chia, trò ra kết quả 0.454545...

Thầy:

- Chính xác. Lại một lần nữa con có số thập phân không kết thúc.Bây giờ, chúng ta tổng kết lại những gì đã làm

½ = 0.5, ¾ = 0.75

1/3 = 0.333.... , 5/11 = 0.454545...

Con có nhận xét gì về việc chuyển đổi phân số ra số thập phân không?

.......

Thầy:

- Con thấy có hai trường hợp khác nhau không? Trường hợp ½ và ¾ khác với trường hợp 1/3 và 5/11

Trò:

- ½ và ¾ khi đổi sẽ ra số thập phân kết thúc. Còn...1/3 và 5/11 khi đổi ra số thập phân kéo dài hoài không kết thúc.

Thầy:

- Quá giỏi. Con phát biểu cực kỳ chính xác. Riêng trường hợp số thập phân không kết thúc, con con có nhận xét gì về các con số không?

Trò:

- Hình như các số nó cứ lặp đi lặp lại

Thầy:

- Quá giỏi. Và các nhà toán học gọi tên nó là số thập phân lặp đi lặp lại (recurring decimal). Vậy ta đúc kết lại như sau: khi đổi một phân số ra số thập phân, ta có hai trường hợp: số thập phân kết thúc (terminating decimal) và số thập phân không kết thúc lập đi lập lại (recurring decimal). Con đã tìm ra được một kết luận mà các nhà toán học thời cổ đại đã mất rất nhiều thời gian để khám phá ra.

Cuộc đối thoại nói trên chỉ là một khái quát hóa những trao đổi giữa thầy và trò trong thực tế. Tùy theo căn cơ của người học trò mà nó có thể dài hoặc ngắn hơn. Nhưng tôi tin rằng nếu người thầy khéo léo dẫn dắt học trò tự mình làm việc với cây bút và tờ giấy để đi đến được kết luận như trên thì con em chúng ta sẽ không thể nào quên được các khái niệm phân số, số thập phân kết thúc và số thập phân lặp đi lặp lại. Điều quan trọng hơn nữa là con em chúng ta đã chạm được cái cảm giác hạnh phúc của sự khám phá. Cái cảm giác lâng lâng tự hào ấy sẽ là một trải nghiệm không thể nào quên của các con. Nó là một nhân tố giúp con cảm thấy thích học toán hơn. Nếu duy trì được cách dạy và học như vậy, khi lớn lên, đứa trẻ sẽ có khuynh hướng khám phá điều mới lạ không chỉ trong môn toán mà trong công việc và sự nghiệp sau này.

Bạn hãy tưởng tượng sự trao đổi giữa thầy và trò diễn ra với một máy tính cầm tay, lạnh lùng hiển thị kết quả số thập phân và lại làm tròn kết quả. Nó dập tắt một cách đáng tiếc mọi hứng khởi đáng ra phải được khơi dậy trong tâm trí trẻ thơ.

(còn tiếp...)

VÌ SAO KỲ THI TOÁN GCSE CAMBRIDGE YÊU CẦU THÍ SINH KHÔNG ĐƯỢC DÙNG MÁY TÍNH CẦM TAY? (Phần 4)

https://www.facebook.com/share/p/gi389SH24Hdeuttw/

Người thầy giỏi là người biết cách truyền đạt kiến thức cho học sinh hiểu, nắm chắc các khái niệm, ứng dụng các định lý trong chương trình đang học và có kỹ năng tính toán tốt để đạt điểm cao trong những kỳ thi kiểm tra.

Người thầy có tâm là người luôn hiểu rằng đằng sau các khái niệm toán học và định lý khô khan là cả một thế giới đầy thú vị, giúp trẻ rèn luyện khả năng tư duy, gợi mở và duy trì lòng ham muốn khám phá của trẻ.

Người thầy có tâm, giỏi lại thêm kinh nghiệm là người phải biết cân đối lượng thời gian đang có cùng với căn cơ riêng biệt của trẻ, vừa giúp trẻ hoàn thành nhiệm vụ học ở trường, đạt điểm cao nhưng không bỏ qua những cơ hội giúp trẻ chạm vào niềm vui khám phá, yêu thích sự tìm tòi và tạo ra khác biệt.

Tiếc thay, việc tìm một người thầy như vậy không phải là dễ.

Động lực đầu tiên khiến các con phải học là điểm số. Đứa trẻ sẽ ham học hơn nếu nó thấy việc học giúp điểm số được cải thiện, bạn bè nể phục, có cơ hội ra oai và chém gió với bạn cùng lớp. Nhưng dần dà, sẽ đến lúc trẻ cảm thấy nhàm chán với điểm số lúc nào cũng đạt mức A hoặc A* và mất dần hứng thú. Chỉ có niềm vui khám phá, hạnh phúc phát hiện và cảm nhận hoa thơm cỏ lạ trên hành trình học mới là động lực miên viễn của một đời người.

Tệ hại nhất là nhồi nhét đầu con/em một lượng kiến thức vô hồn, không lý giải, ép trẻ thuộc lòng cách giải một số dạng toán mẫu nhằm đối phó với kỳ thi. Dạy như vậy thà không dạy còn hơn. Trẻ học theo lối này sẽ không có một chút cảm hứng nào với môn học, lâu dần mất luôn tư duy phản biện, hứng thú sáng tạo, khám phá, chỉ còn là một đứa trẻ răm rắp thuộc lòng, lớn lên thành một robot mê tín, nô lệ tư tường.

Đương thời, đức Phật luôn nêu cao tinh thần tự do tư tưởng. Ngài không ép buộc mọi người phải tin ngay vào những gì Ngài nói. Trong bài kinh “Các vị ở Kesaputta” thuộc Phẩm lớn, chương Ba pháp, Tăng chi bộ kinh, đức Thế Tôn đã thuyết cho người Kalama ở Kesaputta đại ý như sau:

Một là, chớ vội tin một điều gì, chỉ vì điều đó là truyền thuyết.

Hai là, chớ vội tin một điều gì, chỉ vì điều đó thuộc về truyền thống.

Ba là, chớ vội tin một điều gì, chỉ vì điều đó được nhiều người nhắc đến hay tuyên truyền.

Bốn là, chớ vội tin một điều gì, chỉ vì điều đó được ghi lại trong kinh điển hay sách vở.

Năm là, chớ vội tin một điều gì, chỉ vì điều đó thuộc lý luận siêu hình.

Sáu là, chớ vội tin một điều gì , chỉ vì điều đó phù hợp với một lập trường nào đó.

Bảy là, chớ vội tin một điều gì, khi mà điều đó được căn cứ trên những dữ liệu được đánh giá một cách hời hợt.

Tám là, chớ vội tin một điều gì, chỉ vì điều ấy phù hợp với định kiến của mình.

Chín là, chớ vội tin một điều gì, chỉ vì điều ấy được sức mạnh và quyền uy ủng hộ.

Mười là, chớ vội tin một điều gì, chỉ vì điều ấy được các nhà truyền giáo hay đạo sư của mình tuyên thuyết.

Toán học và khoa học là công cụ tuyệt vời để giáo dục con bạn về tinh thần độc lập tư tưởng, về tư duy phản biện logic và là một trong những phương cách giúp con bạn tận hưởng hạnh phúc khám phá, sáng tạo.

Hãy để con chim nhỏ trong vòng tay bạn được tiếp cận, được giáo dục để trưởng thành theo cách của một đại bàng sải cánh bay tự do, dường như không giới hạn trong bầu trời tư tưởng vô biên.

(còn tiếp...)

Jun 05, 2024

CHƯƠNG TRÌNH IGCSE MATHS 0580 CỦA CAMBRIDGE THAY ĐỔI